61 Дано действительное число x. Получить целую часть числа x (*); затем - число x,
округленное до ближайшего целого; затем - число x без дробных цифр.
62 Определить, является ли данное целое число четным.
63 Определить, верно ли, что при делении неотрицательного целого числа a на положительное целое число b получается остаток, равный одному из двух заданных чисел r или s.
64 Дано натуральное число n (n > 99). Определить число сотен в нем.
65 Дано натуральное число n (n ≤ 99). Выяснить, верно ли, что n2 равно кубу суммы цифр числа n.
66 Даны целые числа k, m, действительные числа x, y, z. При k < m2, k = m2, k > m2 заменить модулем соответственно значения x, y или z, а два других значения уменьшить на 0,5.
67 Дано натуральное число n (n ≤ 100).
68 Дано натуральное число n (n ≤ 9999).
69 Часовая стрелка образует угол φ с лучом, проходящим через центр и через точку,соответствующую 12 часам на циферблате,0 < φ ≤ 2π . Определить значение угла для минутной стрелки, а также количество часов и полных минут.
70 Даны целые числа m, n (0< m ≤ 12, 0 ≤ n < 60) указывающие момент времени: «m часов, n минут». Определить наименьшее время (число полных минут), которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате
71 Дано действительное число а. Вычислить f(a), где f — периодическая функция с периодом 1.5, совпадающая на отрезке [0, 1.5]:
72 Дано действительное число а. Вычислить f(a), где f—периодическая функция с периодом 2, совпадающая на отрезке [—1, 1]:
73 Даны целые числа k, l. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
74 Дано натуральное число n (n ≤ 100), определяющее возраст человека (в годах). Дать для этого числа наименования «год», «года» или «лет»: например, 1 год, 23 года, 45 лет и т. д.
75 Доказать, что любую целочисленную денежную сумму, большую 7 руб., можно выплатить без сдачи трешками и пятерками. Для данного n > 7 найти такие целые неотрицательные а и b, что Зa + 5b = n.
76 Поле шахматной доски определяется парой натуральных чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа k, l, m, n, каждое из которых не превосходит восьми. Требуется:
(*) Целой частью числа x, обозначаемой [x], называется наибольшее целое, не превосходящее x;
так, [3.14] = 3, [3] = 3, [-3.14] = -4, [-3] = -3.
62 Определить, является ли данное целое число четным.
63 Определить, верно ли, что при делении неотрицательного целого числа a на положительное целое число b получается остаток, равный одному из двух заданных чисел r или s.
64 Дано натуральное число n (n > 99). Определить число сотен в нем.
65 Дано натуральное число n (n ≤ 99). Выяснить, верно ли, что n2 равно кубу суммы цифр числа n.
66 Даны целые числа k, m, действительные числа x, y, z. При k < m2, k = m2, k > m2 заменить модулем соответственно значения x, y или z, а два других значения уменьшить на 0,5.
67 Дано натуральное число n (n ≤ 100).
-
а) Сколько цифр в числе n?
б) Чему равна сумма его цифр?
в) Найти последнюю цифру числа n.
г) Найти первую цифру числа n.
д) В предположении, что n ≥ 10, найти предпоследнюю цифру числа n.
68 Дано натуральное число n (n ≤ 9999).
-
а) Является ли это число палиндромом (перевертышем) с учетем четырех цифр, как, например,
числа 2222, 6116, 0440 и т.д.?
б) Верно ли, что это цисло содержит ровно три одинаковые цифры, как, например, числа 6676, 4544, 0006 и т.д.?
в) Верно ли, что все четыре цифры числа различны?
69 Часовая стрелка образует угол φ с лучом, проходящим через центр и через точку,соответствующую 12 часам на циферблате,0 < φ ≤ 2π . Определить значение угла для минутной стрелки, а также количество часов и полных минут.
70 Даны целые числа m, n (0< m ≤ 12, 0 ≤ n < 60) указывающие момент времени: «m часов, n минут». Определить наименьшее время (число полных минут), которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате
-
а) совпадут;
б) расположатся перпендикулярно друг к другу.
71 Дано действительное число а. Вычислить f(a), где f — периодическая функция с периодом 1.5, совпадающая на отрезке [0, 1.5]:
-
а) с функцией х3 — 2.25x;
б) с функцией, график которой изображен на рис. 4
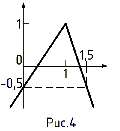
72 Дано действительное число а. Вычислить f(a), где f—периодическая функция с периодом 2, совпадающая на отрезке [—1, 1]:
-
а) с функцией — x2 + 1;
б) с функцией, график которой изображен на рис. 5
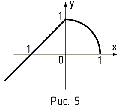
73 Даны целые числа k, l. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
74 Дано натуральное число n (n ≤ 100), определяющее возраст человека (в годах). Дать для этого числа наименования «год», «года» или «лет»: например, 1 год, 23 года, 45 лет и т. д.
75 Доказать, что любую целочисленную денежную сумму, большую 7 руб., можно выплатить без сдачи трешками и пятерками. Для данного n > 7 найти такие целые неотрицательные а и b, что Зa + 5b = n.
76 Поле шахматной доски определяется парой натуральных чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа k, l, m, n, каждое из которых не превосходит восьми. Требуется:
-
а) Выяснить, являются ли поля (k, l) и (m, n) полями одного цвета.
б) На поле (k, l) расположен ферзь. Угрожает ли он полю (m, n)?
в) Аналогично б), но ферзь заменяется на коня.
г) Выяснить, можно ли с поля (k, l) одним ходом ладьи попасть на поле (m, n). Если нет, то выяснить, как это можно сделать за два хода (указать поле, на которое приводит первый ход).
д) Аналогично г), но ладья заменяется на ферзя.
е) Аналогично г), но ладья заменяется на слона.
- Предполагается, что указанные поля имеют один и тот же цвет.
(*) Целой частью числа x, обозначаемой [x], называется наибольшее целое, не превосходящее x;
так, [3.14] = 3, [3] = 3, [-3.14] = -4, [-3] = -3.
 Предыдущая глава
Предыдущая глава